MAを深掘りしていて、指数平滑移動平均線(EMA)の計算式と意味が謎過ぎたので、中学レベル?高校レベル?の数学で解き明かしてみるよ。
こんなの知らなくてもFXはできるよ(/・ω・)/hahaha
移動平均線(MA)はこちらの記事でまとめているよ

EMAの式
式はこれ。
EMA = ひとつ前のEMA + 2/(n+1) × (現在価格 – ひとつ前のEMA)
1本前のEMAが算出できないときは、最初だけSMAと同じ式を使う。
SMA = n本の価格の合計 /n
これらの式に、適用価格を古い順にx1,x2,x3,…として、計算してみるぞ。
最初のEMA
「5EMA」を計算していくことにする。
最初はSMAと同じ式を使うので、
EMA=(x1+x2+x3+x4+x5)/5
このあと、どんどんややこしくなるので、最初のEMAは”E”とおく。
2つ目以降のEMA
式に当てはめると、n=5なので
平滑化定数a = 2/(5+1) = 1/3
になるのだけど…まずはとりあえず、
2/(n+1) = a
と置いて、計算していくことにする。
2つ目の5EMA
現在の終値に x6 を代入して
5EMA
= E + a ( x6 – E )
= E + ax6 – aE
= ax6 + (1-a)E
3つ目の5EMA
現在の終値に x7 を代入して、
5EMA
= { ax6 + (1-a)E } + a [ x7 – { ax6 + (1-a)E }]
= ax6 + (1-a)E + ax7 – a²x6 – a(1-a)E
= ax7 + a(1-a)x6 + (1-a)²E
4つ目の5EMA
現在の終値に x8 を代入して、
5EMA
= { ax7 + a(1-a)x6 + (1-a)²E } + a [ x8 – { ax7 + a(1-a)x6 + (1-a)²E ]
= ax7 + a(1-a)x6 + (1-a)²E + ax8 -a²x7 -a²(1-a)x6 – a(1-a)²E
= ax8 + a(1-a)x7 + a(1-a)²x6 + (1-a)³E
5つ目の5EMA
現在の終値に x9 を代入して、
5EMA
= { ax8 + a(1-a)x7 + a(1-a)²x6 + (1-a)³E } + a [ x9 – { ax8 + a(1-a)x7 + a(1-a)²x6 + (1-a)³E }]
= ax8 + a(1-a)x7 + a(1-a)²x6 + (1-a)³E + ax9 – a²x8 – a²(1-a)x7 – a²(1-a)²x6 + a(1-a)³*E
= ax9 + a(1-a)x8 + a(1-a)²x7 + a(1-a)³x6 + (1-a)^4*E
6つ目の5EMA
現在の終値に x10 を代入して、
5EMA
= { ax9 + a(1-a)x8 + a(1-a)²x7 + a(1-a)³x6 + (1-a)^4*E } + a [ x10 – { ax9 + a(1-a)x8 + a(1-a)²x7 + a(1-a)³x6 + (1-a)^4*E }]
= ax9 + a(1-a)x8 + a(1-a)²x7 + a(1-a)³x6 + (1-a)^5*E + ax10 – a²x9 – a²(1-a)x8 – a²(1-a)²x7 – a²(1-a)³x6 – a(1-a)^4*E
= ax10 + a(1-a)x9 + a(1-a)²x8 + a(1-a)³x7 + a(1-a)^4*x6 + a(1-a)^5*E
小まとめ:EMAの式はこうなる!
平滑化定数 a = 2/(n+1) と置くと
nEMA
= a × 最新価格 + a(1-a) × 1つ前の価格 + a(1-a)² × 2つ前の価格 + a(1-a)³ × 3つ前の価格 + …
わかった?わかりそう???
ちなみに、nは自然数(1以上の整数)なので、
平滑化定数 a = 2/(n+1) <1になる。
…
やっぱりわけわかんないわ( ;∀;)
解説を試みるね!(‘◇’)ゞ
EMAの式からわかること
適用価格n本分のnEMAの式を↓のようにした理由をまとめていく。
nEMA
= a × 最新価格 + a(1-a) × 1つ前の価格 + a(1-a)² × 2つ前の価格 + a(1-a)³ × 3つ前の価格…
※ a = 2/(n+1)
最初のEMAとした”E”はどこへ…?
最初のEMAであるEの係数の推移を見てみる。
| EMA | 1つ目 | 2つ目 | 3つ目 | 4つ目 | 5つ目 | 6つ目 |
| Eの係数 | 1 | (1-a) | (1-a)² | (1-a)³ | (1-a)^4 | (1-a)^5 |
ここからNつ目のEの係数は、
Eの係数 = (1-a)^(N-1)
になると推察される。
nもNも自然数なので
(1-a) < 1 ※ a = 2/(n+1)
であるため、N→∞ のとき (1 – a)^(N – 1)は限りなく0に近づく。
参考に n=5 の時、グラフはこんな感じになる(※ x = N-1 とする)
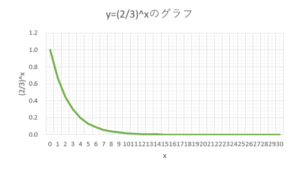
から、Eは無視していいと思うのよ(*’ω’*)←
仮で置いただけだし…
いつか消えてなくなるので、削っちゃったよ。
2/(n+1)の意味は?
2/(n+1)は、平滑化定数。らしい。
EMAについて調べていると、こんな式を紹介しているサイトもあった。
EMA ≒ ( n本の価格の合計 + 最新の価格 )/(n+1)
…平滑化定数ってこれじゃん(; ・`д・´)←?
より新しい価格を重要視して、計算するのがEMAなので…EMAの式として紹介するのは…違う気がする…けど近い値にはなるのかな?
要は最新の価格を重視するために2回足して、その倍にした分、分母が1増える…のよ。
価格の重み付け具合を可視化!
n本よりも前の価格も反映されている!?
EMAの式から、赤字部分を計算して、円グラフに落とし込む。
nEMA = a × 最新価格 + a(1-a) × 1つ前の価格 + a(1-a)² × 2つ前の価格 + a(1-a)³ × 3つ前の価格…
赤字部分の合計は1になるはずなので…円グラフの合計は1になるように調整したよ(‘◇’)ゞ
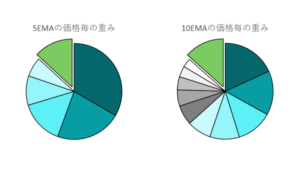
最新価格が青→薄くなるにつれて古い価格の反映度。
そしてこれにびっくりした!
緑の部分は、n本より前の価格が占める割合。
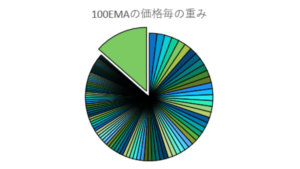
計算してみてびっくりしたのだけど、nEMAは、n本より前の価格も数値に反映されているっぽい。
n本より前の価格が占める割合はnによって少し変わるのだけど、大体13~14%になった。
最新の価格と過去の価格の重みづけの変化
EMAの式から、赤字部分を計算して、そのままグラフに落とす。
nEMA = a × 最新価格 + a(1-a) × 1つ前の価格 + a(1-a)² × 2つ前の価格 + a(1-a)³ × 3つ前の価格…
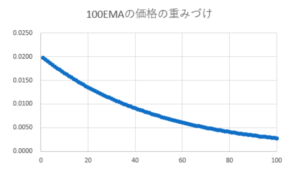
より新しい価格を重視しているのが見て取れるね(‘◇’)ゞ
まとめ
EMA = ひとつ前のEMA + 2/(n+1) × (現在価格 – ひとつ前のEMA)
EMAの式とされるこの式を変形していくと
nEMA = a × 最新価格 + a(1-a) × 1つ前の価格 + a(1-a)² × 2つ前の価格 + a(1-a)³ × 3つ前の価格…
※ a = 2/(n+1)
という式で表すことができる。
そしてどうやら、nEMAのn本分の価格よりもさらに過去の価格も(一応)反映されたMAっぽい…!
それでいて、多少古い価格になると、係数がどんどん0に近くなる…
(どっかで計算を間違えてなければ…なにか間違えてたら指摘してほしいぜ…)
単純移動平均線(SMA)より、最新の価格変化に敏感でありつつも、さらに過去の価格の影響も拾ってくれる指数平滑移動平均線(EMA)って結構最強なのか…???
人気があるというのも頷ける。
まあね!意味が分かっても使いこなせなきゃ意味ないですからね!
脱線はこのくらいにしようね~(*’ω’*)hahaha




